Hyper-parameter scans

Many regression methods involve hyper parameters that need to be tuned to obtain optimal results. Here, we demonstarate how the choice of some of these hyper parameters influences the resulting model. The accuracy of the models is evaluated using the CrossValidationEstimator.

In the following cell we set up the cluster space and compile the structures from the randomized training set.

from icet import ClusterSpace, StructureContainer
from ase.io import read
from ase.db import connect

# set up ClusterSpace and StructureContainer
cutoffs = [9.0, 5.0]
prim = read('../structures/MoC_rocksalt_prim.xyz')
chemical_symbols = [['C', 'Be'], ['Mo', 'V']]
cs = ClusterSpace(prim, cutoffs, chemical_symbols)
sc = StructureContainer(cs)

# collect training structures
db = connect('../dft-databases/rocksalt_MoVCvac_randomized.db')
for row in db.select():
    structure = row.toatoms()
    sc.add_structure(
        structure,
        properties=dict(mixing_energy=row.mixing_energy))
A, y = sc.get_fit_data(key='mixing_energy')

Next we set up the parameters for the three different fit methods considered here, namely automatic relevance detection regression (ARDR), least-absolute-shrinkage-and-selection-operator (LASSO) regression, and recursive feature eliminatiom (RFE).

For each of these methods we specify the range over which to scan the respective hyper parameter. In the case of LASSO and RFE we also specify some additional fit parameters.

import numpy as np

# set up hyper-parameter ranges
n_parameters = A.shape[1]
fit_methods = dict()
fit_methods['ardr'] = ('threshold_lambda', np.logspace(0.5, 5, 25))
fit_methods['rfe'] = ('n_features', np.arange(2, n_parameters, 2))
fit_methods['lasso'] = ('alpha', np.logspace(-4.0, 0, 25))

# additional fit parameters
fit_kwargs = {}
fit_kwargs['lasso'] = dict(max_iter=50000, tol=1e-4)
fit_kwargs['rfe'] = dict(step=1)

Now we loop over the fit methods and hyper parameters, and compile the results into a DataFrame that will be used below for plotting the results.

from pandas import DataFrame
from trainstation import CrossValidationEstimator

# number of splits used for cross validation
n_splits = 20

# number of structures used for training
train_size = 100

data = []
for fit_method, (hp_name, hp_value_range) in fit_methods.items():
    for hp_value in hp_value_range:

        kwargs = fit_kwargs.get(fit_method, {}).copy()
        kwargs[hp_name] = hp_value
        cve = CrossValidationEstimator(
            (A, y), fit_method=fit_method, n_splits=n_splits,
            train_size=train_size, validation_method='shuffle-split',
            **kwargs)
        cve.train()
        cve.validate()

        data.append(dict(
            fit_method=fit_method,
            train_size=train_size,
            n_parameters=cve.n_parameters,
            hyper_parameter_name=hp_name,
            hyper_parameter_value=hp_value,
            n_nonzero_parameters=cve.n_nonzero_parameters_splits.mean(),
            rmse_validation=cve.rmse_validation,
            rmse_train=cve.rmse_train,
        ))

df_all = DataFrame(data)

Some warnings ...

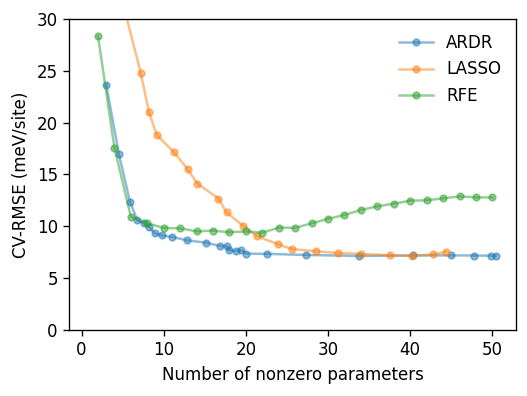
Finally we plot the cross-validated root mean square error (CV-RMSE) as a function of the nonzero parameters for each fit method. The results show that RFE and in particular ARDR yield both accurate and sparse models, whereas LASSO has a (well-known) tendency to overselect for this type of regression problem.

from matplotlib import pyplot as plt

fig, ax = plt.subplots(
    figsize=(4.5, 3.4),
    dpi=120,
)

for fit_method, df in df_all.groupby('fit_method'):
    ax.plot(df.n_nonzero_parameters, 1e3 * df.rmse_validation,
            '-o', label=fit_method.upper(), alpha=0.5, ms=4)

ax.set_xlabel('Number of nonzero parameters')
ax.set_ylabel('CV-RMSE (meV/site)')
ax.set_ylim(0, 30)
ax.legend(frameon=False)

fig.tight_layout()