Cutoff selection

One of the most important tasks when constructing a cluster expansion is the choice of appropriate cutoffs. A simple way to select cutoffs is to scan a wide range of different values and monitor how the cross validation error changes, as will be demonstrated below.

Here, we will use the randomized dataset for the \(\ce{Mo_{1-x}V_xC_{1-y}}\) system.

from ase.db import connect
from ase.io import read

# setup
chemical_symbols = [['C', 'Be'], ['Mo', 'V']]
db = connect('../dft-databases/rocksalt_MoVCvac_randomized.db')
prim = read('../structures/MoC_rocksalt_prim.xyz')

# collect training structures
training_structures = []
for row in db.select():
    structure = row.toatoms()
    structure.info['mixing_energy'] = row.mixing_energy
    training_structures.append(structure)

from icet import ClusterSpace, StructureContainer

def get_fit_data(cutoffs: list[float]):
    """ Helper function for compiling the sensing matrix and
    target mixing energies given a set of cutoffs. """
    cs = ClusterSpace(prim, cutoffs, chemical_symbols)
    sc = StructureContainer(cs)
    for structure in training_structures:
        sc.add_structure(
            structure,
            properties=dict(mixing_energy=structure.info['mixing_energy']))
    return sc.get_fit_data(key='mixing_energy')

Selecting the pair cutoff

Next, we loop over different pairwise cutoffs and compute the cross-validation.

import numpy as np
from pandas import DataFrame
from trainstation import CrossValidationEstimator

# parameters
fit_method = 'ardr'
train_size = 350
n_splits = 300
cutoff_pair_vals = [4, 5, 6, 7, 8, 9, 10, 11, 12]

# run pair cutoff scan
records = []
for c2 in cutoff_pair_vals:
    print(f'pair cutoff: {c2:4.1f}')
    A, y = get_fit_data([c2])

    cve = CrossValidationEstimator(
        (A, y), validation_method='shuffle-split', n_splits=n_splits,
        fit_method=fit_method, train_size=train_size)
    cve.train()
    cve.validate()

    records.append(dict(
        cutoff_pair=c2,
        rmse_train=cve.rmse_train,
        rmse_validation=cve.rmse_validation,
        n_parameters=cve.n_parameters,
    ))

df2 = DataFrame(records)

pair cutoff:  4.0
pair cutoff:  5.0
pair cutoff:  6.0
pair cutoff:  7.0
pair cutoff:  8.0
pair cutoff:  9.0
pair cutoff: 10.0
pair cutoff: 11.0
pair cutoff: 12.0

from matplotlib import pyplot as plt

fig, ax = plt.subplots(
    figsize=(4.5, 3.4),
    dpi=120,
)

ax.plot(df2.cutoff_pair, 1e3 * df2.rmse_train,
        '--s', label='training error')
ax.plot(df2.cutoff_pair, 1e3 * df2.rmse_validation,
        '-o', label='validation error')
ax.set_xlabel('Pair cutoff (Å)')
ax.set_ylabel('RMSE (meV/site)')
ax.set_ylim(0, 15)

ax2 = ax.twinx()
ax2.plot(df2.cutoff_pair, df2.n_parameters,
         ':d', color='tab:red', label='number of parameters')
ax2.set_ylim(0, 60)
ax2.set_ylabel('Number of parameters')

ax.plot(np.nan, np.nan, ':d', color='tab:red', label='number of parameters')
ax.legend(loc='upper center')

fig.tight_layout()

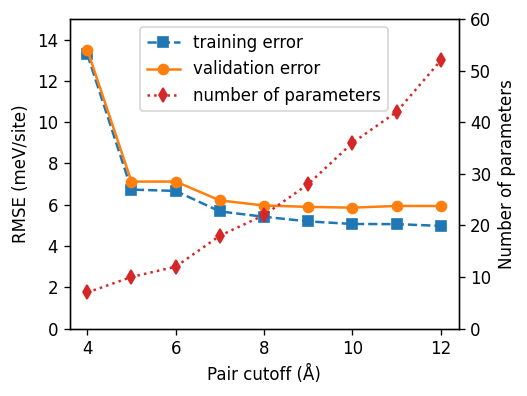
From the above figure it is apparent that the validation error does not improve beyond 9 Å. In fact it even increases slightly again. This indicates that a suitable choice for the pair cutoff is 9 Å.

Selecting the triplet cutoff

Next, we repeat the same procedure for the triplet cutoff using a fixed pair cutoff of 9 Å.

cutoff_pair_final = 9.0
cutoff_triplet_vals = [3, 4, 5, 6, 7]
records = []
for c3 in cutoff_triplet_vals:
    print(f'cutoff triplet: {c3}')
    A, y = get_fit_data([cutoff_pair_final, c3])

    cve = CrossValidationEstimator(
        (A, y), validation_method='shuffle-split', n_splits=n_splits,
        fit_method=fit_method, train_size=train_size)
    cve.train()
    cve.validate()

    records.append(dict(
        cutoff_triplet=c3,
        rmse_train=cve.rmse_train,
        rmse_validation=cve.rmse_validation,
        n_parameters=cve.n_parameters,
    ))

df3 = DataFrame(records)

cutoff triplet: 3
cutoff triplet: 4
cutoff triplet: 5
cutoff triplet: 6
cutoff triplet: 7

fig, ax = plt.subplots(
    figsize=(4.5, 3.4),
    dpi=120,
)

ax.plot(df3.cutoff_triplet, 1e3 * df3.rmse_train,
        '--s', label='training error')
ax.plot(df3.cutoff_triplet, 1e3 * df3.rmse_validation,
        '-o', label='validation error')
ax.set_ylim(0, 10)
ax.set_xlabel('Triplet cutoff (Å)')
ax.set_ylabel('RMSE (meV/site)')

ax2 = ax.twinx()
ax2.plot(df3.cutoff_triplet, df3.n_parameters,
         ':d', color='tab:red', label='number of parameters')
ax2.set_ylim(0, 150)
ax2.set_ylabel('Number of parameters')

ax.plot(np.nan, np.nan, ':d', color='tab:red', label='number of parameters')
ax.legend(loc='upper left')

fig.tight_layout()

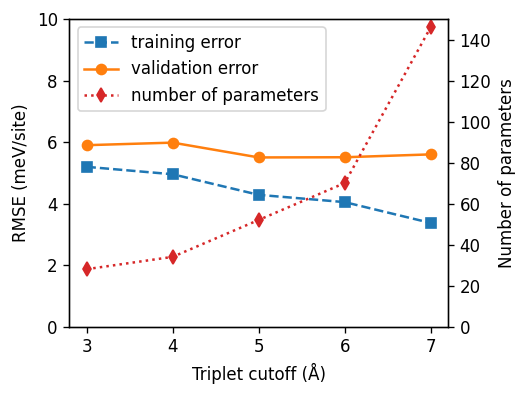
Applying the same logic as in the case of the pair cutoff this analysis indicates a triplet cutoff of 5 Å. This process can be repeated for higher order clusters (quadruplets etc) but in the present case this will not lead to a significant improvement of the model.

In general simpler models (shorter cutoffs) tend to yield more transferable and well-behaved models. In general, selecting cutoffs is not an exact procedure and one needs to balance accuracy vs simplicity of the model.